曾经有一款流行的游戏，叫做 Infinity Loop，先来简单的介绍一下这个游戏:

游戏在一个 $n\times m$ 的网格状棋盘上进行，其中有些小方格中会有水管，水管可能在方格某些方向的边界的中点有接口，所有水管的粗细都相同，所以如果两个相邻方格的公共边界的中点都有接头，那么可以看作这两个接头互相连接。水管有以下 $15$ 种形状：

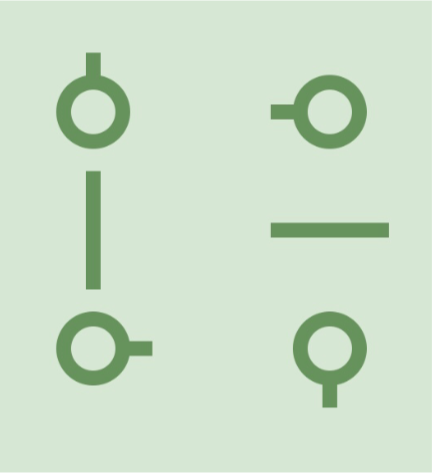
游戏开始时，棋盘中水管可能存在漏水的地方。

形式化地:如果存在某个接头，没有和其它接头相连接，那么它就是一个漏水的地方。

玩家可以进行一种操作：选定一个含有非直线型水管的方格，将其中的水管绕方格中心顺时针或逆时针旋转 $90$ 度。

直线型水管是指左图里中间一行的两种水管。

现给出一个初始局面，请问最少进行多少次操作可以使棋盘上不存在漏水的地方。

第一行两个正整数 $n,m$，代表网格的大小。

接下来 $n$ 行每行 $m$ 个数，每个数是 $[0,15]$ 中的一个，你可以将其看作一个 $4$ 位的二进制数，从低到高每一位分别代表初始局面中这个格子上、右、下、左方向上是否有 水管接头。

特别地，如果这个数是 $0$，则意味着这个位置没有水管。

比如 3(0011(2))3(0011_{(2)})3(0011(2)) 代表上和右有接头，也就是一个 L 型，而 12(1100(2))12(1100_{(2)})12(1100(2)) 代表下和左有接头，也就是将 L 型旋转 $180$ 度。

输出共一行，表示最少操作次数。如果无法达成目标，输出 $-1$.