在一个 sss 个点的图中,存在 s−ns-ns−n 条边,使图中形成了 nnn 个连通块,第 iii 个连通块中有 aia_iai 个点。
现在我们需要再连接 n−1n-1n−1 条边,使该图变成一棵树。对一种连边方案,设原图中第 iii 个连通块连出了 did_idi 条边,那么这棵树 TTT 的价值为:
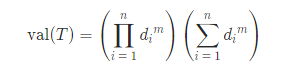
你的任务是求出所有可能的生成树的价值之和,对 998244353998244353998244353 取模。
在一个 sss 个点的图中,存在 s−ns-ns−n 条边,使图中形成了 nnn 个连通块,第 iii 个连通块中有 aia_iai 个点。
现在我们需要再连接 n−1n-1n−1 条边,使该图变成一棵树。对一种连边方案,设原图中第 iii 个连通块连出了 did_idi 条边,那么这棵树 TTT 的价值为:
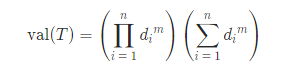
你的任务是求出所有可能的生成树的价值之和,对 998244353998244353998244353 取模。
输入的第一行包含两个整数 n,mn,mn,m,意义见题目描述。
接下来一行有 nnn 个整数,第 iii 个整数表示 aia_iai (1≤ai<998244353)(1\le a_i< 998244353)(1≤ai<998244353)。
输出包含一行一个整数,表示答案。
3 1
2 3 41728
本题共有 202020 个测试点,每个测试点 555 分。
20%20\%20% 的数据中,n≤500n\le500n≤500。
另外 20%20\%20% 的数据中,n≤3000n \le 3000n≤3000。
另外 10%10\%10% 的数据中,n≤10010,m=1n \le 10010, m = 1n≤10010,m=1。
另外 10%10\%10%的数据中,n≤10015,m=2n \le 10015,m = 2n≤10015,m=2。
另外 20%20\%20% 的数据中,所有 aia_iai 相等。
100%100\%100% 的数据中,n≤3×104,m≤30n \le 3\times 10^4,m \le 30n≤3×104,m≤30。
其中,每一个部分分的测试点均有一定梯度。